
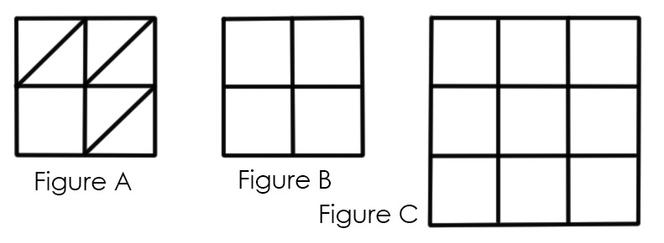
Une énigme classique consiste à essayer de tracer une certaine figure géométrique d’un seul trait, sans lever le crayon et sans repasser plusieurs fois sur la même ligne. Vous pouvez par exemple essayer avec la figure A.
Ce type de tracé est pratiqué et étudié depuis bien longtemps dans différentes régions du monde. Au Vanuatu, la tradition des dessins géométriques dans le sable a été classée au Patrimoine immatériel culturel de l’Unesco en 2008. En Afrique centrale, la tradition idéographique Lusona pourrait dater de plus de deux millénaires. En mathématiques, on nomme ces tracés « chemins eulériens », du nom de Leonhard Euler, mathématicien suisse qui les étudia au XVIIIe siècle.
Mais il peut y avoir un piège : certains dessins sont impossibles ! En voici la raison. A chaque carrefour de la figure, il est possible de compter le nombre de chemins qui s’y rejoignent. Si ce carrefour n’est ni le point de départ, ni le point d’arrivée du tracé, ce nombre de chemins doit être pair, puisque, à chaque passage du tracé, il faut un chemin pour y arriver et un autre pour en repartir. Ainsi, un carrefour où se rejoignent un nombre impair de chemins doit nécessairement être soit le point de départ, soit le point d’arrivée : il ne faut donc pas qu’il y en ait plus que deux !
Il vous reste 34.63% de cet article à lire. La suite est réservée aux abonnés.
